Description

Video Fractal is a powerful tool for creating breathtaking videos of the Mandelbrot and Julia sets. The 2D view allows for easy surveying and key framing, and the custom script editor can be used to fine tune each video. Export MPEG-4 videos up to 4096 x 2048 resolution with up to 240 fps and 24 hour lengths using the state of the art ffmpeg library. 2D still exports are also available while the 3D view captures spectacular images that can be exported at up to 16 megapixel resolution. Multi-processor support and an OpenGL powered renderer allow for blazing fast speed. With double precision 64-bit mathematics, Fractal 3D is capable of resolving detailed images up to an incredible 1,000,000,000,000x magnification level! To give perspective, a single atom of carbon magnified one trillion times would be longer than two football fields. Each fractal is fully customizable and changes happening in real time. First adjust the fractal set type, equation power/ constants, iterations, resolution, color scheme, and smoothing options. Once the fractal is rendered it can be explored with intuitive panning and zooming controls. After a place of interest is found, customize the 3D view by rotating the fractal, moving the camera, and adjusting the lighting. Due to the nature of fractals, the number of unique patterns to be found is limitless. Use the rendered images for desktop wallpaper, printed artwork, or just enjoy the beauty of exploring one of a kind images created by pure mathematics.

Fractal information from Wikipedia – A fractal has been defined as “a rough or fragmented geometric shape that can be split into parts, each of which is (at least approximately) a reduced-size copy of the whole,” a property called self-similarity. The term fractal was coined by Benoît Mandelbrot in 1975 and was derived from the Latin fr?ctus meaning “broken” or “fractured.” A mathematical fractal is based on an equation that undergoes iteration, a form of feedback based on recursion. There are several examples of fractals, which are defined as portraying exact self-similarity, quasi self-similarity, or statistical self-similarity. While fractals are a mathematical construct, they are found in nature, which has led to their inclusion in artwork. They are useful in medicine, soil mechanics, seismology, and technical analysis. A fractal often has the following features: It has a fine structure at arbitrarily small scales. It is too irregular to be easily described in traditional Euclidean geometric language. It has a simple and recursive definition. Because they appear similar at all levels of magnification, fractals are often considered to be infinitely complex (in informal terms). Natural objects that are approximated by fractals to a degree include clouds, mountain ranges, lightning bolts, coastlines, snow flakes, various vegetables (cauliflower and broccoli), and animal coloration patterns. However, not all self-similar objects are fractals —for example, the real line (a straight Euclidean line) is formally self-similar but fails to have other fractal characteristics; for instance, it is regular enough to be described in Euclidean terms.

Requirements

• Macintosh running Mac OS 10.8+

Links

• Macintosh
  • Video Fractal App Store

Instructions

• Rendering Video
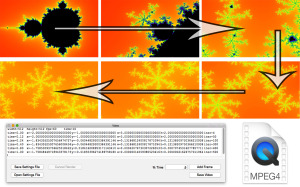
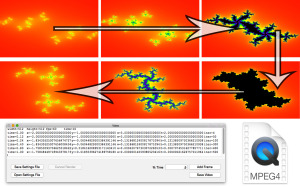
  • Pressing the Save Video button will attempt to run the entered script, saving a video file based on the entered parameters.
  • Press Cancel Render at any time to stop the render
  • A real time preview will be shown as the application works to save the video. This is useful to tweak the parameters before spending time on a long high-resolution render. Progress will also be shown in a text field below the script, showing the current frame and total number of frames to be rendered
  • Scripts can be saved and opened for later modifications using the Save/Open Settings File buttons
• Script Setup
  • Setting up a script includes two steps. Global variables must be set on the first line, followed by individual keyframe parameters
  • The most simple way to build a script is using the Add Frame button. Simply navigate the preview window to the desired result and press the Add Frame button to add a line to the script. Make sure to set the time before pressing Add Frame, time is expressed as a percentage from 0.00 to 1.00
  • Values can then be hand tweaked and re-ordered as necessary before rendering
  • Global Variables
    • width=512 – Horizontal resolution of the rendered file
    • height=512 – Vertical resolution
    • fps=60 – Frames per second. Older monitors typically refresh at 30 frames per second while newer displays usually refresh 60 times per second
    • time-10 – Length of the finished video, in seconds.
    • The time it takes a computer to render will be directly proportional to these variables. In the example above 600 total frames will be rendered at 512×512 resolution, taking a minute or so on modern computers.
    • All other variables will default to the values in the Settings panel, including but not limited to Color Scheme, Equation, and Set Type
  • Keyframes – Video Fractal will interpolate between keyframes, they must be in chronological order based on time
    • time=0.00 – Time, expressed as a percentage of the global time length. The most simple script would start at time=0.00 and end at time=1.00. More complicated scripts add additional keyframes between 0.00 and 1.00
    • x=, y= – X and Y coordinates of the rendered region
    • w=, h= – Width and height lengths of the rendered region
    • iter= – Maximum iterations for each fractal
    • cReal=, cImg= – Constants used for Julia sets, not necessary in Mandelbrot sets
• General Information
  • Experiment with different settings. Using small resolution settings along with short overall time lengths will speed up the process
  • Typos in scripts or invalid keyframe times can cause the application to misbehave
  • Save script changes before rendering in case of an application crash

Screenshots

 

Videos